中国数学·魏晋南北朝数学
魏晋南北朝是指从三国到隋文帝统一中国之前的时代,在此期间,中国数学的各项成就达到了高峰,而中国数学的传统、特色也有了明确的显示。
三国时代吴人赵爽,字君卿,身世不详。曾为《周髀》作注,在“注” 中,有 “负薪余日,聊观《周髀》”之类语句,依此而论,赵爽当是一介寒儒。他不但补绘了“日高图”及“七衡图”;他还撰写了“勾股圆方图”注、“日高图”注、“七衡图”注;在“勾股圆方图”注中,他用五百余字,论证了勾股原理,并论证了有关勾、股、弦的二十多条命题,在“日高图”注中,他对所谓“日高术”即重差术,也给予几何证明,在“七衡图”注中,他对盖天学说的理论作了说明,所有这些,对后世研讨《周髀》者都有很大裨益。例如“勾股圆方图”注说:“勾、股各自乘,并之为弦实。开方除之,即弦。案弦图又可以勾、股相乘为朱实二,倍之为朱实四。以勾、股之差自相乘为中黄实。加差实一,亦成弦实。”其前一句是重复论述勾股原理,而后一句则是以面积概念证明了勾股原理 (图5)。即:
设勾、股、弦分别为a、b、c,勾股原理即:
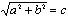
其证明过程为:
勾、股相乘为朱实二 ab
倍之为朱实四 2ab
以勾、股之差自相乘为中黄实 (b-a)2
加差实一,亦成弦实 2ab+ (b-a)2=c2
这是中国对勾股原理第一次严密的证明。
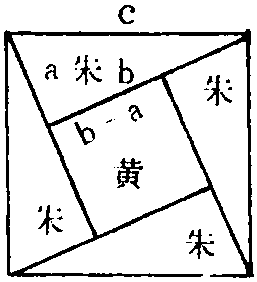
图5
在“日高图”下,赵爽注说:“黄甲与黄乙其实正等。以表高乘两表相去为黄甲之实。以影差为黄乙之广而一,所得,则变得黄乙之袤,上与日齐。按图当加表高,今言八万里者,从表以上复加之。青丙与青己其实亦等。黄甲与青丙相连,黄乙与青己相连,其实亦等”。这是中国古代推求日高的传统方法,一般称为“重差术”,就是在平地上立两根等高的表,当日光照射两表时,两表即有表影。根据两表相对位置、高度、影长便可求得日高。其计算公式为:
日高=[ (表高×两表间距离)
÷两表之影差] +表高
为了说明这一算法的正确性,赵爽给予严密的证明(图6):
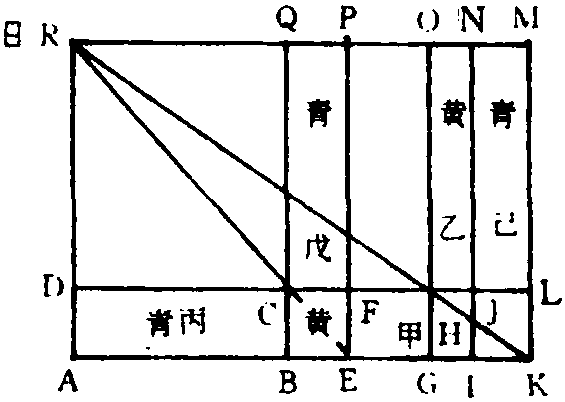
图6
黄甲与黄乙其实正等 □BH=□HN
以表高乘两表相去为黄甲之实 BC×BG=□BH
以影差为黄乙之广而一 □HN÷(GK-BE)=HO
所得则变得黄乙之袤,上与日齐 HO=(BC×BG)÷(GK-BE)
按图当加表高 AR=[(BC×BG)÷(GK-BE)]+BC
今言八万里者,从表上复加之 其中所说“八万里”,是《周髀》所推算的日高数字
青丙与青己其实亦等 □AC=□JM
黄甲与青丙相连,黄乙与青
已相连,其实亦等 □AC+□BH=□HN+□JM
赵爽可能根据这样等积关系证明上述日高公式的:长方形的一条对角线,将长方形分割成等积的两部分,因而可得右上小长方形与左下小长方形等积(图7)。赵爽对日高公式的论证,为重差理论的发展奠定了坚实的基础。
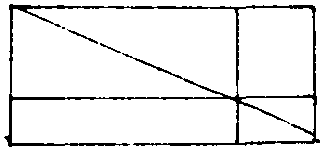
图7
在《周髀算经注》中,赵爽不但在数学方面作了精采的阐述,还写出了珍贵的治学之道;他说“累,重也。若诚能重累思之,则达至微之理”。在数学研究上,他主张“累思”;只有累思才能贯通各种道理。他还说“凡教之道,不愤不启,不悱不发;愤之,悱之,然后启发,……,举一隅,使反之以三也”。在数学的学习中,不仅要独立思考,而且还要举一反三。只有这样才能收到良好的教益。
略晚于赵爽的是刘徽。刘徽是魏、晋期间杰出布衣数学家,其身世不详,经初步考证,当是现今山东人,曾为《九章算术》作过注解; 刘徽《九章算术注》中,在数学理论上、方法上、技巧上、程序上多所建树和发明,为中国数学奠定了传统的理论基础,为中国数学形成了独特的理论体系,其铮铮之词,铿锵有声。
刘徽利用 “出入相补原理”,即图形的分、合、移、补的方法证明平面图形如圭田、邪田、箕田、圆田、宛田、弧田、环田的面积算法,还用以证明勾股原理。《九章·方田》圭田术为“半广以乘正从”。刘徽注称“半广者,以盈补虚为直田也。亦可半正从以乘广。按半广乘从,以取中平之数。故广、从相乘为积步”。刘徽把“圭田”即等腰三角形割补成长方形,依据长方形的面积算法推证“圭田”的面积算法(图8)。故得:
圭田面积=1/2×(广)×(正从)=1/2×(正从)×(广)
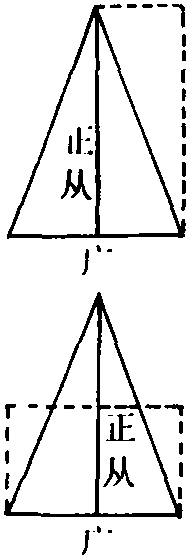
图8
《九章·勾股》勾股术为“勾股各自乘,并而开方除之,即弦”。刘徽注称:“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也。合成弦方之幂,开方除之,即弦也。”其证明方法,就是把勾方之“朱出”部分,补入“朱入”之处;再把股方之“青出”部分,补入“青入”部分;便合成了弦方。开平方求其边长,即得其弦长 (图9)。即:
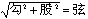
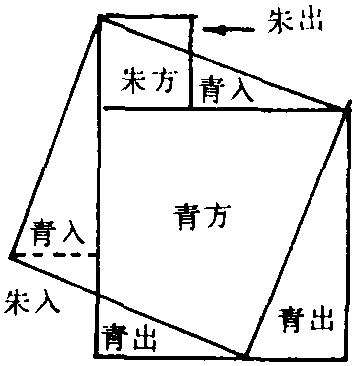
图9
刘徽还利用面积理论证明了可以与希腊哲学家毕达哥拉斯(Pythagoras,约公元前580—500)、哲学家柏拉图(Plato,公元前427—347)以及数学家欧几里得(Euclid,约公元前330—275)相媲美的整数勾股弦的一般公式。
设勾、股、弦分别为a、b、c,整数勾股弦一般公式为:
a∶b∶c=[m2-(1/2)(m2+n2)]
∶mn∶(1/2) (m2+n2)
关于直线型平面图形的面积算法,刘徽都是以“出入相补原理”证明的。对于圆型平面图形如圆田、弧田的面积算法,刘徽则是利用极限观念和出入相补原理也即所谓“割圆术”证明其面积算法,并求得圆周率较精密之值分别为:
π=157/50=3.14
π=3927/1250=3.1416
对于环田,乃是将环田之周拉直,使变为等积的梯形,再用出入相补原理证明其面积算法。在算法理论上、数学思想上,刘徽的这一套理论和方法是十分珍贵的。
刘徽把环田之周拉直,使之变形为等积的梯形。实际上这是一种“化曲为直”或“以直代曲”的思想,这种思想一方面体现在《九章》商功章“曲池术”下注文中,他说“此池环而不通匝,表如盘蛇而曲之。亦云周者,谓如委谷依垣之周耳。引而伸之,周为袤,求袤之意,环田也”。一方面体现在《九章》勾股章“葛之缠木术”下注文中,他说“以笔管青线宛转有似葛之缠木,解而观之,则每周之间,自有相间成勾股弦”。也即是说,他不但把一些平面曲线即圆弧拉成直线,还把空间曲线即柱面螺旋线拉成直线。刘徽这种思想成为中国数学的一项传统、特色,并影响着后世。
刘徽在推证勾股原理的基础上,还用面积理论推证有关勾、股的各种线段的求法,还用相似勾股形性质推证“勾股容方”、“勾股容圆”的算法,也证明了简单的测量算法。“勾股容方”即是推求直角三角形内接正方形的边长,勾股章第15问为“今有勾五步,股十二步。问勾中容方几何”。术文为“并勾、股为法,勾、股相乘为实,实如法而一,得方一步”。设勾、股分别为a=5,b=12,其内接正方形之边长为x。按术乃得:
x=ab÷(a+b)=5×12÷(5+12)=3+(9/17)
刘徽一方面用相似形性质即比例证明这一算法的正确性,一方面用面积理论证明这一算法的合理性。“勾股容圆”即是推求直角三角形内切圆的直径,勾股章第16问为“今有勾八步,股十五步。问勾中容圆,径几何”。术文为“八步为勾,十五步为股,为之求弦。三位并之为法,以勾乘股,倍之为实。实如法得径一步”。设勾、股分别为a=8,b=15,弦为c,内切圆直径为d,按术乃得:
d =2ab÷ (a+b+c)
=2×8×15÷ (8+15+17) =6
其中c=
 =17。刘徽是一方面用“出入相补原理”证明此算法,一方面用相似形性质推证此算法,在注文之末,又给予推求内切圆直径的四种算法。即:
=17。刘徽是一方面用“出入相补原理”证明此算法,一方面用相似形性质推证此算法,在注文之末,又给予推求内切圆直径的四种算法。即:d=a-(c-b)
d=b-(c-a)
d=(a+b)-c
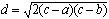
刘徽对于直线型柱体如城、垣、堤、沟、堑、渠的体积或容积算法,也以“出入相补原理”予以证明;他把“出入相补原理”作为一条普遍原理,几乎应用于全部的几何中。刘徽又利用三种基本几何体,即堑堵、阳马、鳖臑,先证明三种基本几何体的体积算法,再把直线型非柱体的立体分割为三种基本几何体,然后证明其体积或容积的算法。可见,他把三种基本几何体作为多面体体积算法的理论关键。例如,他推证方亭体积,即正四棱台体积时,把方亭分割为一长方体、四堑堵、四阳马,由长方体、阳马、鳖臑的体积算法,推证方亭的体积算法为:
方亭= (1/3) (上方2+上方×下方+下方2) ×高
其中“上方”、“下方”分别是正四棱台的上、下底边之长。又如他把方锥,即正四棱锥分割为四个阳马,由阳马的体积算法,推证方锥的体积算法为:
方锥= (1/3) ×下方2×高
其中“下方”即是方锥下底之边长。再如,对于羡除、刍甍、刍童、盘池等立体,也都是分割为若干个三种基本几何体进行论证的。
刘徽在推证圆型立体体积算法时,采用了“截割原理”,即是在圆柱、圆锥、圆台上,分别作一外切方柱、方锥、方台,以圆型立体与其外切方型立体体积之比为π∶4,于是,可从方型立体的体积算法推证得圆型立体的体积算法。如刘徽推证圆亭体积,即正圆台的体积时,其算法为:
圆亭=(1/3)(1/4π)(上周2+上周×下周
+下周2)×高
=(π/4)方亭
=(π/4)[(1/3)(上方2+上方×下方
+下方2)×高]
其中“上周”、“下周”分别是圆亭上、下底之周长。而“上方”、“下方”分别是圆亭外切正四棱台上底、下底一边之长。在《九章》中,一般取圆率为π=3。又如他推证圆锥体积,即正圆锥体积时,其算法为:
圆锥= (1/3) (1/4π) (下周2) ×高
=(π/4) 方锥= (π/4) [ (1/3) ×
(下方2) ×高]
其中“下周”即圆锥下底之周长,“下方”即圆锥外切方锥下底之边长。刘徽在推求圆型立体体积运算中,提出圆柱、圆亭、圆锥、与其外切方柱、方亭、方锥体积之比为π∶4,这是十分正确的论断,不但对推算圆型立体体积给予了一条捷径,而且是中国数学的一项突出成就。在推求球体积问题上,刘徽取一正方体,在正方体内作相互垂直的两圆柱面,称两圆柱的公共部分为“牟合方盖”,再在“牟合方盖”里作一内切球,他深知“牟合方盖”与其内切球体积之比为4∶π。虽然他未能求得球体积的算法,但提出“牟合方盖”与其内切球体积之比,在算法理论上、数学思想上都是十分珍贵的。
在代数方面,刘徽也有不少杰出的贡献。例如,他对分数、正负数及其运算都有独到的论述,对于某些无理数即二次根数也有逼近的描述。在实数领域中,可以说中国古代已形成基本的体系。《九章》对“方程”即所谓线性方程组的解法,原是“直除法”,即是连续相减的消元法,刘徽把“直除法”推广为“互乘对减”的加减消元法,并提出消去常数项法;使线性方程组的解法达到尽善尽美的地步。对于衰分算法、等比级数、等差级数、调和级数等项,都有创新工作。他还明确地给予等差级数的求和公式、通项公式、公差公式。即:
Sn=[a1+(n-1)(d/2)]×n
=n·a1+[n(n-1)]×(d/2)
an=a1+ (n-1) ×d
d= (am-an) ÷ (m-n)
其中“Sn”、“a1”、“n”、“d”、“an”以及“am”分别是等差级数的前n项之和、首项、项数、公差、第n项以及第m项。
刘徽对数学名词改变了“约定俗成”的惯例,对一些名词给予明确的定义,如把“率”定义为“凡数相与者,谓之率”。“等除法实,相与率也”。即是说,凡数与数之比,称之为“率”,约简两数之比,则称为“相与率”。并把“率”概念几乎应用到所有算法之中,作为各种算法的主线。给正负数所下定义为:“今两算得失相反,要令正负以名之。”还给“方程”下了正确的定义,既给出“方程”有确切解的条件,又给出 “方程”的同解理论,并创造性的给出 “方程”的新解法。此外,刘徽还对幂、齐同通、列衰、开平方、开立方、鳖臑、阳马、堑堵、勾、股、弦等数学名词都给出正确的定义。刘徽的这些定义,不但没有含混不清之词,也没有循环定义之举,都合于逻辑,因而成为演绎论证的理论依据。刘徽在推理演绎与证明方法上,既有归纳,也有演绎;既有综合法,也有分析法,还有反证法; 在逻辑方面是十分丰富的。在中国数学理论的发展上,形成了第一次高峰。
西汉时期,主张盖天学说的天文学家创造了测量日高、远的方法,称之为重差术,到刘徽时代,几乎失传。刘徽乃潜心研究测量原理,使重差术加以发展,并由两次测望推广至三次、四次测望,编撰九道测量问题,缀于《九章算术》之终。他说“辄造《重差》,并为注解,以究古人之意,缀于《勾股》之下。度高者重表,测深者累矩,孤离者三望,离而又旁求者四望”。唐代,李淳风为国子监审定数学教材,使另行单本,因其第一问为“今有望海岛”,故称之为《海岛算经》。可见刘徽在测量理论上的成就是卓著的。
生活在南北朝宋、齐时代的著名数学家祖冲之及其子祖暅,对数学有很出色的贡献,例如他们父子曾作《缀术》一书,可惜早已失传。保留至今的,只有祖冲之所创造的圆周率,即:
介于盈朒二限:3.1415926<π<3.1415927
密率:π=355/113
约率:π=22/7
还有其子祖暅解决了刘徽所提出的“牟合方盖”体积问题,从而得到球体积的巧妙证法。
在南北朝成书的数学名著有《孙子算经》及《张邱建算经》。《孙子算经》三卷,是一部数学普及著作,其中著名的问题有卷下“鸡兔同笼”问题和“物不知数”问题。“鸡兔同笼”题称:“今有雉兔同笼,上有三十五头,下有九十四足。问雉兔各几何。”“术曰:上置三十五头,下置九十四足。半其足得四十七。以少减多,再命之,上三除下四,上五除下七。下有一除上三,下有二除上五,即得。又术曰:上置头,下置足。半其足,以头除足,以足除头,即得。”表示以现代形式,即:
| 上头 35 下足 94 | 35 | 35 35-12=23(雉) |
| 半足94÷2=47(双) | 47 47-35=12 | 12(兔) |
实即:(94÷2)-35=12 即是兔头数35-12=23
即是雉头数
这种问题实际是现今所谓“带余除法”算法的延续;也是小学算术教材中难题“鸡兔同笼”题的最早记载。“物不知数”题称:“今有物,不知其数。三三数之,剩二;五五数之,剩三;七七数之,剩二。问物几何。”也即现今之一次同余式组问题。表示以现代形式,设所求物数为N,则有:
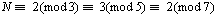
《孙子算经》给出N的最小解为N=23。西方学者一直称这问题为“中国剩余定理”,我们则称之为“孙子定理”。
《张邱建算经》也是一部数学普及著作,书中涉及最大公约数和最小公倍数的正确求法,还有七道问题涉及等差级数及其解法,有的固然是继承了《九章》的成果,但在等差级数方面,有更多的内容则是创新。如求出自然数之和、等差级数前n项之和、公差公式、通项公式、项数公式等,其形式分别为:
1+2+3+……+n=n(n-1)/2
Sn=(n/2)(a1+an)
d=2[(Sn/n)-a1]÷(n-1)
a1=an-(n-1) d
Sn=na1+n (n-1) (d/2)
n= [2 (m-a1) +d] ÷d
其中“n”、“Sn”、“a1”、“an”、“d”、“m”,分别是等差级数的项数、前n项之和、首项、末项、公差、前n项的算术平均值。在《张邱建算经》卷下,有一“百鸡问题”,是著名的不定方程问题,即:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。凡百钱买鸡百只,问鸡翁、母雏各几何。”其术文过于简略,只说“鸡翁每增四,鸡母每减七,鸡雏每益三。即得”。所以很难通晓其具体算法。今以现代解法论述如次:设鸡翁、鸡母、鸡雏的只数分别为x、y、z,依题意得:
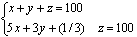
《张邱建算经》给出三组答案,即是:
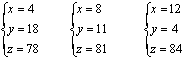
实际上相当于指出这一不定方程组的解是:x=4t,y=25-7t,z=75+3t。(其中参数t分别取1、2、3,即得其解。)书中所给三组答案,虽然《九章算术》已有不定方程的记载,但一题给以数种答却始自《张邱建算经》。
在南北朝时代,还出现了较为通俗的数学著作,计有《五曹算经》、《五经算术》以及《数术记遗》等书。而《五曹算经》,是一部为地方行政官员所编写的应用算术手册,全书分为五卷,分别是“田曹”、“兵曹”、“集曹”、“仓曹”、“金曹”,其中共列有67道算术问题,其解法都很浅近,在计算中所用数字,好像有意避免使用分数;在“田曹”中,除了长方形、三角形、平行四边形的面积计算公式正确外,其他腰鼓形、鼓形、四不等形的面积算法都是错误的。其《五经算术》,是把《诗》、《书》、《周礼》、《仪礼》、《礼记》、《论语》以及《左传》里有关数字计算的问题,加以解说,虽然对于经学的研究有所帮助,但有些解说不免过于穿凿附会。而《数术记遗》则是一部脱离现实的书,其中讨论了 “三等数”,认为 “上数”是累进制,即:“上数者,数穷则变,若言万万曰亿,亿亿曰兆,兆兆曰京也。”“中数”是万万进制,即:“中数者,万万变之,若言万万曰亿,万万亿曰兆,万万兆曰京也。”“下数”是十进制,即:“下数者,十十变之,若言十万曰亿,十亿曰兆,十兆曰京也。”并把数分为“十等”,即亿、兆、京、垓、秭、壤、沟、涧、正、载。还列举了十四种不同记数法:即“积算”、“太乙算”、“两仪算”、“三才算”、“五行算”、“八卦算”、“九宫算”、“运筹算”、“了知算”、“成数算”、“把头算”、“龟算”、“珠算”、“计数算”等。
以上所述,就是中国数学在魏晋南北朝的辉煌成就。尤其是在三国时代,数学家赵爽及刘徽的贡献与成就,使中国数学达到了辉煌的境界,从而形成中国数学的第一次高峰。



上一篇:三通学·踵作诸书——从“九通”到“十通”
下一篇:申韩学·现代申韩学研究·国内申韩学